나무는 뿌리에서 시작하여 줄기를 타고 여러 개의 가지로 뻗는다. 각각의 가지는 다시 여러 개의 가지로 뻗고, 이 과정을 몇 번 반복한다. 그리고 가지의 끝에는 나뭇잎이나 열매가 맺히게 된다. 이러한 나무의 구조와 유사한 형태의 자료구조를 트리라고 한다.
트리도 앞서 설명한 나무의 구조와 마찬가지로 뿌리(root node)를 시작으로 여러 노드로 분기한다. 각각의 노드는 다시 여러 노드로 분기하며 이러한 과정을 반복하게 된다. 그리고 더 이상 노드로 분기하지 않는 노드를 단말 노드(terminal node 또는 leaf node)라고 한다. 앞서 가지에 끝에 달린 나뭇잎이나 열매와 같은 개념이다. 이러한 트리는 계층을 갖는데, 이는 큐나 리스트와 같은 선형 자료 구조와 구별되는 특징이다. 이러한 특징을 이용해 데이터 관리, 탐색, 러신 머닝 등에 널리 사용된다.

위 그림에서 확인할 수 있는 트리의 구조는 다음과 같다.
- 노드(node): 트리에서 실제 데이터가 저장되는 각각의 요소
(타원형으로 표시) - 간선(edge): 노드와 노드를 연결하는 선
(실선으로 표시) - 부모 노드(parent node): 어떤 노드로부터 여러 개의 노드로 분기될 때, 어떤 노드에 해당되는 노드
(예를 들어 그림에서 G의 부모 노드는 C) - 자식 노드(children node): 어떤 노드로부터 여러 개의 노드로 분기될 때, 여러 개의 노드에 해당되는 노드
(예를 들어 A의 부모 노드는 B, C, D) - 루트 노드(root node): 부모 노드가 없는 노드
(A) - 단말 노드(terminal node. leaf node): 자식 노드가 없는 노드
(J, K, L) - 차수(degree): 어떤 노드로부터 분기된 자식 노드의 수
(예를 들어 G의 차수는 2) - 레벨(level): 트리의 각 층에 순서를 매긴 것
(왼쪽에 표시) - 서브 트리(subtree): 어떤 노드(루트 노드)에서 분기된 노드를 루트 노드로 갖는 트리
(예를 들어 A의 서브 트리는 그림에서 막힌 점선으로 표시된 3개의 트리)
트리에는 다양한 종류가 있는데, 그중 자료 구조에서 주로 이진 트리가 사용된다. 이진 트리는 모든 노드의 차수가 2 이하인 트리를 일컫는다. 이러한 이진 트리에도 몇 가지 종류가 있는데 다음과 같다.
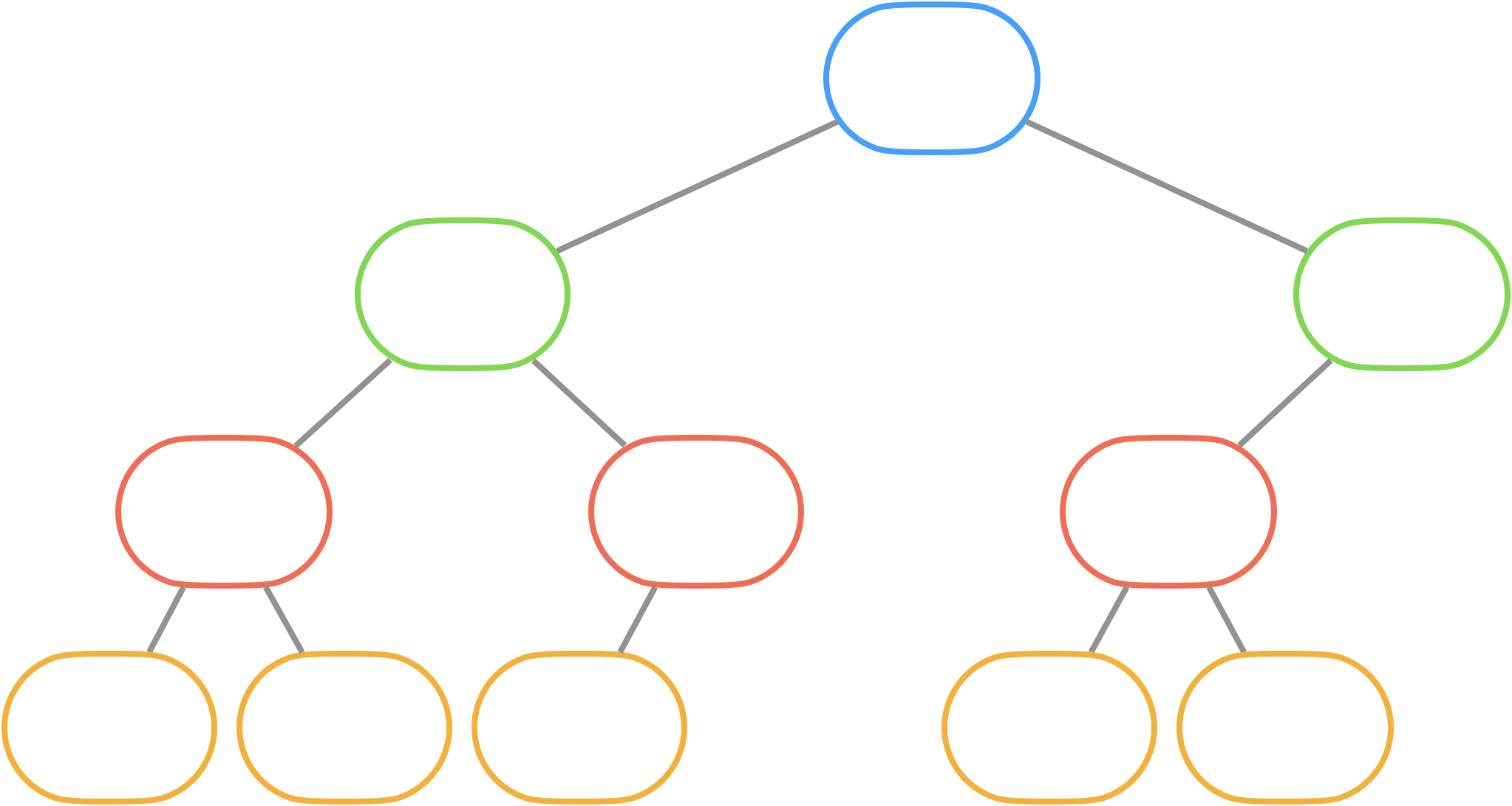
- 완전 이진 트리: 마지막 레벨을 제외한 모든 레벨의 노드가 채워져 있으며, 마지막 레벨에서는 노드가 왼쪽부터 순서대로 채워져 있는 이진 트리

완전 이진 트리의 예시 - 이진 탐색 트리: 각각의 노드의 값이 왼쪽 서브 트리보다는 크고 오른쪽 서브 트리보다는 작은 이진 트리로 노드의 값(키)은 유일하다.

이진 탐색 트리의 예시 - 힙: 단말 노드가 아닌 각각의 노드에 대해 노드의 값이 자식 노드의 값과 비교해 일정한 규칙을 갖는 완전 이진 트리로 노드의 값(키)은 중복 가능하다. 아래의 예시는 Max Heap의 예시로, 모든 부모 노드의 값이 모든 자식 노드의 값이 크다.

힙의 예시
'Computer Science > 데이터 구조' 카테고리의 다른 글
| [Swift] Array를 이용한 Heap 구현 2 - 최대 힙 (0) | 2021.06.03 |
|---|---|
| [Swift] Array를 이용한 Heap 구현 1 - 개요 (0) | 2021.06.03 |
| [Swift] Linked List를 이용한 List 구현 (0) | 2021.06.01 |
| [Swift] Linked List를 이용한 Queue 구현 (0) | 2021.05.28 |
| [Swift] Linked List 구현 (0) | 2021.05.27 |


