허프만 코딩(Huffman Coding)은 이전 포스팅(https://taeminator1.tistory.com/49)에서 언급한 "더 짧은 심벌 트릭(shorter-symbol trick)"의 일종이다. 더 짧은 심벌 트릭은 압축하려는 문자열에서 자주 사용되는 문자일수록 짧은 심벌을 부여하여 압축하는 방법이다. 허프만 코딩은 이러한 심벌을 허프만 코드를 이용해서 압축하는 방법이다.
허프만 코딩의 핵심은 아무래도 허프만 코드를 구하는 것이다. 허프만 코드를 구하는 방법을 살펴보기 전에, "더 짧은 심벌 트릭"에서 "심벌"이 되기 위한 조건을 살펴보자. 다음과 같은 두 가지 조건이 있다.
- 빈도수가 많을수록 심벌의 자릿수가 적어야 한다
- 임의의 심벌이 다른 심벌의 첫 부분이 아니어야 한다
먼저 첫 번째 조건은 앞에서 설명한 "더 짧은 심벌 트릭"의 정의에 포함되어 있어 당연한 말이다. 더 짧은 심벌 트릭으로 압축할 때, 데이터의 양을 줄이기 위해서는 자주 사용되는 문자에 더 짧은 심벌을 부여해야 한다.
두 번째 조건은 압축된 데이터에서 원래 데이터를 추출할 때 필요하다. 예를 들어, 압축된 데이터가 "1000"이고, 우리가 가지고 있는 심벌이 "0", "1", "00"이라고 한다면, 압축된 데이터의 첫 번째 수인 "1"은 심벌 "1"과 바로 대응될 수 있지만, 뒤의 "000"은 심벌과 대응시킬 수 있는 경우가 다음과 같이 3가지 경우가 있다.
- "0" "0" "0"
- "0" "00"
- "00" "0"
이러한 각각의 경우에 대해 다른 결과가 도출되므로 임의의 심벌이 다른 심벌의 첫 부분이 아니어야 한다.
앞에서 설명한 두 가지 조건을 모두 충족시키는 코드 중 하나가 바로 허프만 코드다. 다음으로 허프만 코드를 생성시키는 방법을 살펴보고, 어떻게 해당 방법으로 도출된 코드가 앞의 두 조건을 모두 만족하는 "심벌"이 될 수 있는지 살펴보겠다.
먼저 허프만 코드는 다음과 같은 과정을 통해 도출된다.
- 문자열을 구성하는 문자들에 대한 빈도수를 구하고 각각의 문자들에 대한 노드 생성
- 부모 노드가 없는 노드들 중 빈도수가 적은 두 노드를 선택
- 선택된 두 노드의 빈도수를 더한 값에 대한 새로운 노드를 선택된 두 노드의 부모 노드로 생성
- 부모 노드가 없는 노드가 한 개가 될 때까지 2 단계와 3 단계를 반복
- 루트 노드부터 간선의 방향에 따라 0 또는 1을 대응시켜 최종적으로 각 문자에 대한 허프만 코드 도출
만약 문자열 "bab bdca adcb ba daba ad ab acab ca ab dd"가 주어졌을 때, 문자열을 구성하는 각각의 문자에 대한 허프만 코드를 도출해 보자.
[1 단계: 문자열을 구성하는 문자들에 대한 빈도수를 구하고 각각의 문자들에 대한 노드 생성]

[2 단계: 부모 노드가 없는 노드들 중 빈도수가 적은 두 노드를 선택]
여기서는 4를 갖는 노드와 6을 갖는 노드가 선택된다.

[3 단계: 선택된 두 노드의 빈도수를 더한 값에 대한 새로운 노드를 선택된 두 노드의 부모 노드로 생성]
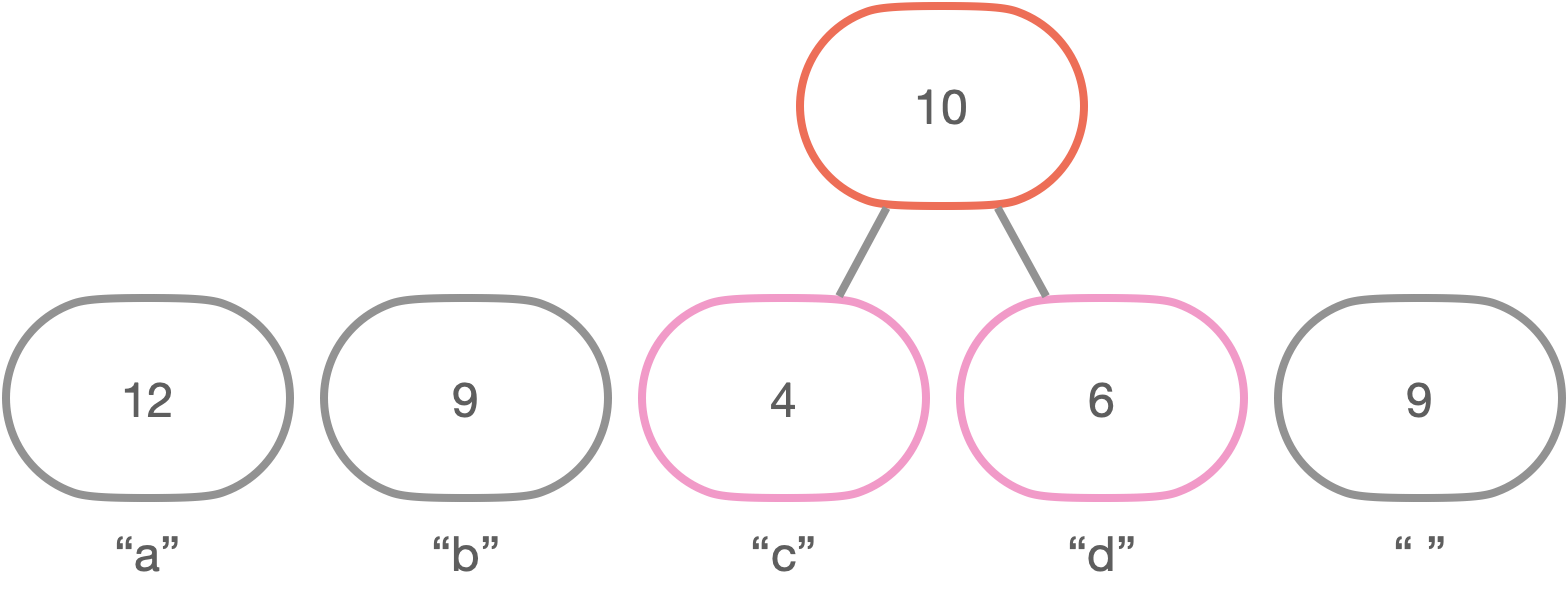
[4 단계: 부모 노드가 없는 노드가 한 개가 될 때까지 2 단계와 3 단계를 반복]
그럼 아래 오른쪽과 같이 최종 트리를 얻을 수 있다.

[5 단계: 루트 노드부터 간선의 방향에 따라 0 또는 1을 대응시켜 최종적으로 각 문자에 대한 허프만 코드 도출]
5 단계를 진행하기 전에, 최종적으로 얻은 트리를 보기 좋게 정리했다. (이 작업은 생략해도 상관없다)

그럼 각각의 문자에 대한 허프만 코드를 다음과 같이 0과 1로 이루어진 수로 도출할 수 있다. 허프만 코드는 트리를 어떻게 배치하느냐에 따라(간선의 방향이 달라지는 것에 따라) 다르게 도출될 수 있다. 허프만 코드를 구성하는 숫자 자체가 중요한 것이 아니라 앞에서 말한 두 조건의 성립 여부가 중요한 것이기 때문에 어떤 식으로 배치를 해도 상관없다.
- "a": 01
- "b": 10
- "c": 000
- "d": 001
- " ": 11
그렇다면 도출된 허프만 코드가 어떻게 앞의 두 조건을 모두 만족하는 코드가 되는 것인지 살펴보자.
[첫 번째 조건: 빈도수가 많을수록 심벌의 자릿수가 적어야 한다]
허프만 코드를 구하기 위한 트리를 생성하는 과정에서 노드의 값이 가장 작은 두 노드를 선택하여 부모 노드를 생성시켰다. 그렇기 때문에, 값이 작을수록 더 많은 간선을 거치게 되고, 간선을 거치는 횟수는 곧 코드의 자릿수가 된다. 따라서 허프만 코드는 첫 번째 조건을 만족한다.
[두 번째 조건: 임의의 심벌이 다른 심벌의 첫 부분이 아니어야 한다]
예를 통해 살펴보자. 임의의 코드 "xxx"가 있을 때, 해당 코드에 0과 1을 뒤에 붙여 만들 수 있는 코드는 "xxx0" 또는 "xxx1"이다. 새롭게 도출된 코드와 기존의 코드가 함께 심벌이 될 수 있을까?? 다시 말해 "xxx", "xxx0", "xxx1"이 함께 심벌이 될 수 있을까?? 답은 당연히 "안 된다"이다. 왜냐하면 "xxx"가 이미 "xxx0" 또는 "xxx1"의 앞부분에 포함되어 있기 때문이다.
따라서 문자열을 구성하는 문자들의 종류만큼 심벌이 추가되어야 하므로 심벌의 개수가 부족하다면, "xxx" 심벌을 폐기하고 "xxx0"과 "xxx1"을 심벌로 추가해야 할 것이다.
이것을 루트 노드로부터 간선의 방향에 따라 추가되는 "0" 또는 "1"이 결정되는 이진 트리로 생각하면, 실제 심벌로 채택될 수 있는 것은 자식 노드가 없는 단말 노드라는 사실을 알 수 있다. 단말 노드가 아닌 노드들은 자식 노드들의 앞부분에서 이미 자신의 코드를 포함하므로 두 번째 조건을 만족할 수 없다. 이렇듯 이진트리에서 단말 노드에 해당하는 코드를 도출하는 방법은 허프만 코드를 구하는 과정과 동일하다. 따라서 허프만 코드는 두 번째 조건도 만족한다.
이렇게 허프만 코드를 구하는 방법과 허프만 코드가 왜 심벌로서 적절한지를 살펴보았다. 다음 포스팅에서는 허프만 코드를 이용해 실제로 압축하는 방법과 압축된 데이터를 추출하는 방법을 알아볼 것이다.
'Computer Science > 알고리즘' 카테고리의 다른 글
| [Swift] 허프만 코딩 구현 1 - 문자열 압축 (0) | 2021.06.11 |
|---|---|
| 허프만 코딩 2 - 문자열 압축과 추출 (0) | 2021.06.10 |
| 데이터 압축 (0) | 2021.06.09 |
| [Swift]Random Surfer Trick 동작 확인 (0) | 2021.05.30 |
| [Swift]Random Surfer Trick 구현 (0) | 2021.05.30 |


